In the field of bioinformatics, one way to measure similarities between two (or more) sequences of
DNA is to perform
sequence alignment:
"a way of arranging the primary sequences of DNA, RNA, or protein to identify regions of similarity that may
be a consequence of functional, structural, or evolutionary relationships between the sequences."
Think of it this way: you've got two random strands of DNA - how do you know where one starts and one begins?
How do you know if they come from the same organism? A closely related pair? You might use sequence alignment
to see how the two strands might line up in relation to each other - subsequences may indicate similar
functionality, or conservation through evolution.
In "normal" programming terms, you've got a couple of strings and want to find out how you might align them so they they look
as much like one another as possible.
There are plenty of ways to achieve that goal. Since we haven't done much programming on here lately,
I thought it would be nice to focus on two very similar algorithms that do so:
Needleman-Wunsch and
Smith-Waterman.
The idea behind these two algorithms is that we have a scoring scheme we want to maximize as successive
"matches" occur. One popular
substitution matrix for scoring
protein alignment is
BLOSUM62
(and here's
a good PDF describing how BLOSUM came about).
The particular scoring matrix you use will be determined by the goals you want to acheive.
For our purposes, a simple matrix or two will suffice:
@substitution_matrix =
[[" ", "a","c","g","t"],
["a", 1 , 0 , 0 , 0 ],
["c", 0 , 1 , 0 , 0 ],
["g", 0 , 0 , 1 , 0 ],
["t", 0 , 0 , 0 , 1 ]]
@substitution_matrix2 =
[[" ", "s", "e", "n", "d", "a"],
["s", 4 , 0 , 1 , 0 , 1 ],
["e", 0 , 5 , 0 , 2 , -1 ],
["n", 1 , 0 , 6 , 1 , -2 ],
["d", 0 , 2 , 1 , 6 , -2 ],
["a", 1 , -1 , -2 , -2 , 4 ]]
The first
@substitution_matrix is fairly simplistic - give one point for each match, and ignore any mismatches or gaps introduced.
In
@substitution_matrix2
what score should be given if "s" is aligned with "a"? (One.) What if "d" is aligned with another "d"? (Six.)
The substitution matrix is simply a table telling you how to score particular characters when they are in the same position in two
different strings.
After you've determined a scoring scheme, the algorithm starts scoring each pairwise alignment, adding to or
subtracting from the overall score to determine which alignment should be returned. It uses
dynamic programming, storing calculations
in a table to avoid re-computation, which allows it to reverse course after creating the table to find and return
the best alignment.
It feels strange to implement this
as a class, but I did it to make it clear how trivially easy it is to derive Smith-Waterman (SW) from Needleman-Wunsch (NW). One design that jumps out at me would be to have a
SequenceAligner where you can choose which algorithm as a method to run - then SW could use a NW algorithm where
min_score is passed as a parameter to the method. Perhaps you can think of something even better.
Anyway, here's the Ruby class that implements the Needleman-Wunsch algorithm.
class NeedlemanWunsch
@min_score = nil
def initialize(a, b, substitution_matrix, gap_penalty)
@a = a
@b = b
# convert to array if a/b were strings
@a = a.split("") if a.class == String
@b = b.split("") if b.class == String
@sm = substitution_matrix
@gp = gap_penalty
end
def get_best_alignment
construct_score_matrix
return extract_best_alignment_from_score_matrix
end
def construct_score_matrix
return if @score_matrix != nil #return if we've already calculated it
initialize_score_matrix
traverse_score_matrix do |i, j|
if i==0 && j==0
@score_matrix[0][0] = 0
elsif i==0 #if this is a gap penalty square
@score_matrix[0][j] = j * @gp
elsif j==0 #if this is a gap penalty square
@score_matrix[i][0] = i * @gp
else
up = @score_matrix[i-1][j] + @gp
left = @score_matrix[i][j-1] + @gp
#@a and @b are off by 1 because we added cells for gaps in the matrix
diag = @score_matrix[i-1][j-1] + s(@a[i-1], @b[j-1])
max, how = diag, "D"
max, how = up, "U" if up > max
max, how = left, "L" if left > max
@score_matrix[i][j] = max
@score_matrix[i][j] = @min_score if @min_score != nil and max < @min_score
@traceback_matrix[i][j] = how
end
end
end
def extract_best_alignment_from_score_matrix
i = @score_matrix.length-1
j = @score_matrix[0].length-1
left = Array.new
top = Array.new
while i > 0 && j > 0
if @traceback_matrix[i][j] == "D"
left.push(@a[i-1])
top.push(@b[j-1])
i -= 1
j -= 1
elsif @traceback_matrix[i][j] == "L"
left.push "-"
top.push @b[j-1]
j -= 1
elsif @traceback_matrix[i][j] == "U"
left.push @a[i-1]
top.push "-"
i -= 1
else
puts "something strange happened" #this shouldn't happen
end
end
return left.join.upcase.reverse, top.join.upcase.reverse
end
def print_score_visualization
construct_score_matrix
print_as_table(@score_matrix)
end
def print_traceback_matrix
construct_score_matrix
print_as_table(@traceback_matrix)
end
def print_as_table(the_matrix)
puts
puts "a=" + @a.to_s
puts "b=" + @b.to_s
puts
print " "
@b.each_index {|elem| print " " + @b[elem].to_s }
puts ""
traverse_score_matrix do |i, j|
if j==0 and i > 0
print @a[i-1]
elsif j==0
print " "
end
print " " + the_matrix[i][j].to_s
puts "" if j==the_matrix[i].length-1
end
end
def traverse_score_matrix
@score_matrix.each_index do |i|
@score_matrix[i].each_index do |j|
yield(i, j)
end
end
end
def initialize_score_matrix
@score_matrix = Array.new(@a.length+1)
@traceback_matrix = Array.new(@a.length+1)
@score_matrix.each_index do |i|
@score_matrix[i] = Array.new(@b.length+1)
@traceback_matrix[i] = Array.new(@b.length+1)
@traceback_matrix[0].each_index {|j| @traceback_matrix[0][j] = "L" if j!=0 }
end
@traceback_matrix.each_index {|k| @traceback_matrix[k][0] = "U" if k!=0 }
@traceback_matrix[0][0] = "f"
end
def s(a, b) #check the score for bases a. b being aligned
for i in 0..(@sm.length-1)
break if a.downcase == @sm[i][0].downcase
end
for j in 0..(@sm.length-1)
break if b.downcase == @sm[0][j].downcase
end
return @sm[i][j]
end
end
Needleman-Wunsch follows that path, and finds the best global alignment possible. Smith-Waterman truncates
all negative scores to 0, with the idea being that as the alignment score gets smaller, the local alignment
has come to an end. Thus, it's best to view it as a matrix, perhaps with some coloring to help you visualize
the local alignments.
All we really need to get Smith-Waterman from our implementation of Needleman-Wunsch above is this:
class SmithWaterman < NeedlemanWunsch
def initialize(a, b, substitution_matrix, gap_penalty)
@min_score = 0
super(a, b, substitution_matrix, gap_penalty)
end
end
However, it would be nice to be able to get a visualization matrix. This matrix should be able to use windows
of pairs instead of
each and every pair, since there can be thousands or millions or billions of base pairs we're aligning. Let's add a couple of methods to that
effect:
#modify array class to include extract_submatrix method
class Array
def extract_submatrix(row_range, col_range)
self[row_range].transpose[col_range].transpose
end
end
require 'needleman-wunsch'
class SmithWaterman < NeedlemanWunsch
def initialize(a, b, substitution_matrix, gap_penalty)
@min_score = 0
super(a, b, substitution_matrix, gap_penalty)
end
def print_score_visualization(window_size=nil)
return super() if window_size == nil
construct_score_matrix
#score_matrix base indexes
si = 1
#windowed_matrix indexes
wi = 0
windowed_matrix = initialize_windowed_matrix(window_size)
#compute the windows
while (si < @score_matrix.length)
sj = 1
wj = 0
imax = si + window_size-1
imax = @score_matrix.length-1 if imax >= @score_matrix.length
while (sj < @score_matrix[0].length)
jmax = sj + window_size-1
jmax = @score_matrix[0].length-1 if jmax >= @score_matrix[0].length
current_window = @score_matrix.extract_submatrix(si..imax, sj..jmax)
current_window_score = 0
current_window.flatten.each {|elem| current_window_score += elem}
begin
windowed_matrix[wi][wj] = current_window_score
rescue
end
wj += 1
sj += window_size
end
wi += 1
si += window_size
end
#find max score of windowed_matrix
max_score = 0
windowed_matrix.flatten.each{|elem| max_score = elem if elem > max_score}
max_score += 1 #so the max normalized score will be 9 and line up properly
#normalize the windowed matrix to have scores 0-9 relative to percent of max_score
windowed_matrix.each_index do |i|
windowed_matrix[i].each_index do |j|
begin
normalized_score = windowed_matrix[i][j].to_f / max_score * 10
windowed_matrix[i][j] = normalized_score.to_i
rescue
end
end
end
#print the windowed matrix
windowed_matrix.each_index do |i|
windowed_matrix[i].each_index do |j|
print windowed_matrix[i][j].to_s
end
puts
end
end
def initialize_windowed_matrix(window_size)
windowed_matrix = Array.new(((@a.length+1).to_f)/window_size)
windowed_matrix.each_index do |i|
windowed_matrix[i] = Array.new(((@b.length+1).to_f)/window_size)
end
return windowed_matrix
end
end
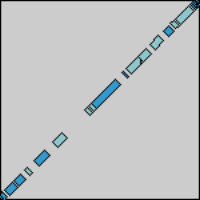
And now we'll try it out. First, we take two sequences and perform a
DNA dotplot analysis on them:

Then, we can take our own visualization, do a search and replace to colorize the results by score, and have a look:
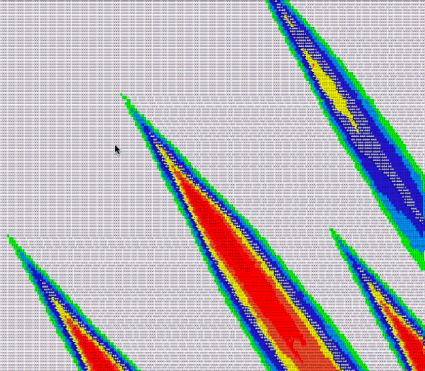
Lo and behold, they look quite similar!
I understand the algorithms are a bit complex and particularly well explained, so I invite questions about
them in particular. As always, comments and (constructive) criticisms are encouraged as well.
Hey! Why don't you make your life easier and subscribe to the full post
or short blurb RSS feed? I'm so confident you'll love my smelly pasta plate
wisdom that I'm offering a no-strings-attached, lifetime money back guarantee!