It was apparent as far back as 1975 that "linear planning" (or totally ordered planning, as described in
What is Partial-Order Planning?) was not sufficient. Russell and Norvig relay the story of Allen Brown's experiment: that it could not solve simple problems such as the Sussman anomaly, where given 3 blocks labeled A, B, and C, with block B on the table and C on top of A which is on the table, get to the goal state of A on top of B on top of C (Russell, 410, 414) (See Figure 1). Around that time, as part of his Ph.D., Austin Tate released a paper which described INTERPLAN, a system to solve the problem of interleaving shown by Brown using Sussman's HACKER program (the Sussman Anomaly) (Tate [A] / Russell 410).
Shortly thereafter, Earl D. Sacerdoti released his paper, "The Nonlinear Nature of Plans" which presented a new data structure to represent plans and gave a glimpse of the first partial order planners, Nets Of Action Hierarchies (NOAH) (and compared that to INTERPLAN, among others) (Sacerdoti, 8).
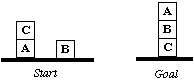
Figure 1. The Sussman Anomaly.
Sacerdoti begins by acknowledging that, "we usually think of plans as linear sequences of actions … because plans are usually executed one step at a time." However, he observed, the "plans themselves are not constrained by limitations of linearity." Because of this, a new structure is needed, which he calls a "procedural net," that would represent "a plan as a partial ordering of actions with respect to time" (Sacerdoti, 1). He backs up his assertion showing the famous Sussman anomaly (described above), and moves on to describe procedural nets and NOAH itself.
Procedural nets are networks of four different types of nodes (GOAL, PHANTOM, SPLIT, and JOIN) and each node represents an action. The nodes are then linked together to form plans. GOAL nodes, clearly, represent a goal that should be achieved. PHANTOM nodes "represent goals that should already be true at the time they are encountered." And, as one might imagine, SPLIT nodes represent splits in the plan, while JOIN nodes represent forks that are coming to an end. Finally, as it is implemented, each of the nodes has a pointer to some code (also known as a closure, lambda expression, or anonymous function) (Sacerdoti, 2).
NOAH uses that structure to represent plans, and a "generic" domain specific language called SOUP (Semantics of a Users' Problem) to give the system knowledge about the task domain (Sacerdoti, 2). To clarify, I call it generic here because it is suitable for describing problems in many domains, but it is specific in that its sole purpose is to describe problems.
To create a new plan, first give NOAH a goal to achieve and tell it about the problem with SOUP. Then it builds a procedural net with only a goal node, which contains a "list of all relevant SOUP functions as its body." Finally, run the planning algorithm. The planning algorithm is described as (quoting Sacerdoti, 3):
- Simulate the most detailed plan in the procedural net. This will have the effect of producing a new, more detailed plan.
- Criticize the new plan, performing any necessary reordering or elimination of redundant operations.
- Go to Step 1.
(Sacerdoti, 3).
Step one is performed in effect by calling the anonymous function pointed to by the node. Step two runs the plan against several critics, namely "Resolve Conflicts," "Use Existing Objects," and "Eliminate Redundant Preconditions," which all perform the actions one would expect from knowing their names (Sacerdoti, 4).
After the release of NOAH, Tate created a new partial order planner dubbed NONLIN. From Sacerdoti, he recognizes "that ordering constraints should only be imposed between the actions comprising a plan if these are necessary for the achievement of the overall purpose of the plan" and bases his work upon it (Tate [B], 889). On the other hand, Tate realized the need for NONLIN because NOAH
still had to make choices as to the order that actions were to be placed-in a plan to correct for interactions. NOAH made this choice in one particular way. It did not keep any backtrack choice points, so this decision, once made, was irreversible. This leads to an incompleteness of the search space which can render some simple block pushing tasks unachieveable (sic) by NOAH… NONLIN is capable of correcting for an interaction by suggesting two orderings (which are sufficient to ensure the incompleteness of NOAH mentioned above is avoided…). (Tate [B], 889)
Additionally, Tate said that "other operations performed by NOAH deterministically … should also be considered as choice points" and gives two examples where "if such decisions cannot be undone, some problems are unsolvable." Of course, NONLIN fixed these problems (Tate [B], 889).
Questions, comments, observations, and critiques on how to improve this are appreciated, as always.
References:
Figure 1: Retrieved on 4/20/2007 from
this place and verified in Russell and Sacerdoti.
Russell, Stuart and Norvig, Peter. Artificial Intelligence: A Modern Approach 2nd Edition. New Jersey: Pearson Education, 2003.
Sacerdoti, Earl D. "The Nonlinear Nature of Plans." 1975. Proceedings of the Fourth International Joint Conference on Artificial Intelligence. Retrieved on 4/20/2007 from
here on the World Wide Web.
Tate, Austin [A]. "INTERPLAN: a plan generation system which can deal with interactions between goals" Research Memorandum MIP-R-109, Edinburgh: Machine Intelligence Research Unit, December 1974. (Can be found online at
here)
Tate, Austin [B]. "Generating Project Networks", Proceedings of the Fifth International Joint Conference on Artificial Intelligence (IJCAI-77) pp. 888-893, Boston, Mass. USA, August 1977. (Can be found online
here)
Hey! Why don't you make your life easier and subscribe to the full post
or short blurb RSS feed? I'm so confident you'll love my smelly pasta plate
wisdom that I'm offering a no-strings-attached, lifetime money back guarantee!
Leave a comment
What about ABSTRIPS? Was the idea of abstraction spaces completely abandoned?
Posted by Artur
on Jan 11, 2008 at 02:19 AM UTC - 6 hrs
Leave a comment